Resumen
Edward Simpson CB dejó de ser un estadístico activo en 1947, cuando se unió al Servicio Civil. Pero las estadísticas le deben mucho. Es el índice de diversidad 1 de Simpson de Simpson y de la paradoja 2 de Simpson , la extraña contradicción aparente que publicó en 1951 y que desde entonces ha desconcertado a los estudiantes de estadística. Quizás más importante, tanto para el mundo como para las estadísticas, desde 1942 hasta 1945 fue un descifrador de códigos en Bletchley Park, donde Alan Turing y otros rompieron los sistemas de cifrado enemigos y se desarrolló la primera computadora moderna del mundo. Aquí Edward Simpson cuenta la historia hasta ahora inédita de la parte que las estadísticas bayesianas jugaron al romper dos de los cifrados enemigos.
Ponencia:
En la actualidad, aunque todavía no se haya entendido universalmente, se creó la primera computadora digital electrónica a gran escala del mundo en Bletchley Park durante la Segunda Guerra Mundial. La introducción allí de Colossus a finales de 1943 transformó el ataque criptoanalítico en el cifrado del teletipo alemán que los descifradores de códigos llamado Tunny permitieron que se leyera.
Tunny era incluso más complejo que el enigma más conocido. La máquina que la cifró fue hecha por la empresa Lorenz. Su tamaño significaba que no era un dispositivo portátil como Enigma. Se usó exclusivamente para los mensajes más importantes que pasaron entre el Alto Mando alemán en Berlín y los comandantes del Grupo de Ejércitos en toda Europa.
A las personas conceptualmente y técnicamente brillantes les costó romperlo. Para nombrar solo a tres de ellos: el sistema de cifrado de Tunny fue resuelto, sin que nadie haya visto la máquina, por Bill Tutte; El concepto y la especificación del procesamiento electrónico de alta velocidad del criptoanálisis y el liderazgo de su aplicación se debieron a Max Newman, ambos en Bletchley Park; El mismo Colossus fue diseñado y construido por Tommy Flowers, por iniciativa propia en primera instancia, en la Estación de Investigación de la Oficina Postal en Dollis Hill. Colossus primero corrió operativamente en Bletchley Park el 5 de febrero de 1944 3 .
El coloso mismo es cada vez más conocido y mejor documentado. Por otro lado, es poco conocido el uso que se hace del teorema de Bayes en varias áreas de trabajo de Bletchley Park, incluida la ruptura del enigma naval alemán en la Choza 8. Ralph Erskine escribe en su Action This Day de "un Bayesian altamente sofisticado". sistema ” 4 ; Hugh Alexander, el campeón de ajedrez que fue un miembro prominente y luego jefe de Hut 8, en su inédita "Historia criptográfica", la pasa por 5 .
He podido reconstruir lo que debe haber sido la contribución de Bayes al ataque a Enigma. Bayes también se usó en Tunny, pero no tengo detalles sobre eso. Pero aquí, porque lo conozco de primera mano, describo el uso hecho de Bayes en el ataque criptoanalítico al principal cifrado naval japonés JN 25 en 1943–1945, por el equipo en el Bloque B que dirigí.
Bayes y naval japonesa 25
El cifrado por JN 25 fue un proceso de dos etapas. La primera etapa fue por un libro de códigos, la segunda por un conjunto de números impresos conocido como tabla de cifrado. El remitente y el destinatario de los mensajes tenían cada uno el libro de códigos y la tabla de cifrado. Usando el libro de códigos, el texto del mensaje se transformó en números, en este caso una serie de grupos de códigos de cinco dígitos. Por lo tanto, la palabra "maru" (envío) podría estar representada por el grupo de códigos 70863. Como verificación contra error, el libro de códigos solo usaba grupos donde la suma de los cinco dígitos era divisible por 3. Coloquialmente, dichos grupos "escanearon". La tabla de cifrado era una amplia gama de números aleatorios de cinco dígitos llamados "aditivos". En la segunda etapa, los grupos de códigos se cifraron colocando junto a ellos una serie de aditivos consecutivos del mismo tamaño tomados de algún lugar de la tabla; y luego añadiendo (no cargando, es decir,1 ).
Una vez que se logró una ruptura inicial, la tarea de los criptoanalistas en Bletchley Park (y sus homólogos estadounidenses y australianos) fue determinar cuáles eran los aditivos y hacerlo lo más rápido posible para que los mensajes interceptados pudieran ser descifrados. La tarea paralela de los creadores de libros (no discutida aquí) fue elaborar los significados textuales de los grupos de códigos como en el libro de códigos japonés.
Los criptoanalistas normalmente tenían en su mesa una "profundidad" de mensajes interceptados, de dos a veinte, que se sabía estaban cifrados en el mismo tramo de aditivos, aunque no todos comenzaban en el mismo lugar. Al alinear correctamente los mensajes uno debajo del otro (lo que podríamos hacer; conocíamos el sistema japonés que lo indicaba) produjo "columnas" de grupos, todos cifrados por los mismos aditivos en sus cabezas. El método principal para recuperar los aditivos comenzó a partir de la observación de que la diferencia (no portadora) entre dos grupos cifrados en una columna será la misma que la diferencia entre los grupos de códigos subyacentes a ellos, porque el aditivo de cifrado (común a los dos) cancela
Como herramienta a su disposición, los criptoanalistas tenían un cuerpo de "buenos grupos" que se sabía que se usaban en el libro de códigos porque habían aparecido en mensajes ya descifrados con éxito, junto con sus frecuencias de ocurrencia. Los mejores de estos grupos buenos conocidos (por ejemplo, los 100 más frecuentes) se diferenciaron entre sí, eligiendo cada vez la alternativa por debajo de 55556. Las 4950 diferencias resultantes se clasificaron en orden numérico, cada una acompañada por los dos grupos buenos que habían producido Es, y tabulado. Para la producción de este "índice de diferencias" confiamos en la instalación masiva de Hollerith que sirvió a todo Bletchley Park. Se trataba de clasificar y tabular la maquinaria que funcionaba leyendo los agujeros perforados en las tarjetas. Herman Hollerith había ideado el sistema medio siglo antes para procesar datos del Censo de los Estados Unidos de 1890.
Tomar de la profundidad una columna de grupos cifrados (por ejemplo, seis profundos) y diferenciarlos uno con el otro produjo un conjunto de diferencias (15 de ellos en este ejemplo). Cada uno fue buscado en el índice. Si estaba allí, un "clic", insertando de nuevo en la columna los dos buenos grupos tabulados con él en el índice liderado por la resta a la identificación de un aditivo especulativo para ir al principio de esa columna (ver Figura 2 ). Los aditivos especulativos así generados tuvieron que ser probados para distinguir lo verdadero de lo falso.
La primera prueba fue simple. Tome A como el aditivo especulativo a ser probado. "Eliminar" la columna significaba restar A (no transportar) de cada grupo cifrado, a su vez, para generar los grupos de códigos descifrados especulativos P, Q, R, ..., incluidos, por supuesto, los dos del índice. Si todo el P, Q, R, ... escaneado, el aditivo especulativo A sobrevivió a la siguiente prueba.
Entre P, Q, R, ... algunos serían conocidos como buenos grupos y otros no. El juicio esencial que se hizo fue si la evidencia colectiva de los buenos grupos que aparecen entre P, Q, R, ... fue lo suficientemente convincente como para que A fuera aceptada como genuina y escrita como "columna resuelta". Este juicio fue tan sutil como la prueba de escaneo fue simple.
Aquellos que hacen este trabajo, una mezcla de civiles y Wrens, fueron rápidos y precisos, pero no formados matemáticamente. Se debían encontrar medios para permitirles emitir juicios de manera rápida y objetiva, estandarizar los juicios en todo el equipo e iniciar nuevos reclutas (ya que el equipo se estaba expandiendo rápidamente) con la menor demora.
Los matemáticos en el equipo de la JN 25 fueron Ian Cassels (más tarde Fellow de Trinity y Sadleirian Professor en Cambridge), Jimmy Whitworth y yo. Nuestra solución para el proceso de juicio requerido comenzó con una aplicación del teorema de Bayes.
La hipótesis a probar era que A era cierta, que este aditivo especulativamente deducido era correcto. Los eventos fueron los grupos de códigos descifrados especulativamente P, Q, R, ... (todo escaneo). Supongamos que Q era un buen grupo. La probabilidad de que Q ocurriera si A era verdadera, p t , se derivó del cuerpo de buenos grupos ensamblados y sus frecuencias de ocurrencia. Si A era falso, Q era solo un número de cinco dígitos de escaneo aleatorio con probabilidad p f de 3: 100 000. El peso de la evidencia proporcionada por Q a favor de que A fuera verdadero era el factor de Bayes p t dividido por p f .
Figura 1
Figura 2
Figura 1
Figura 2
Por motivos prácticos, no había necesidad de agonizar sobre las probabilidades anteriores para ser asignado a la hipótesis de la verdad de A. La evidencia cuantificada en el factor fue suficiente. De manera similar, si (digamos) R no era un buen grupo, este evento tendría una probabilidad un poco menor que la aleatoria si A fuera cierto y un factor resultante un poco por debajo de 1. Pero en una etapa en la que solo una pequeña fracción de los grupos en El libro de códigos era conocido, la desviación por debajo de 1 iba a ser pequeña; por lo tanto, al cambiar este pequeño grado de precisión por velocidad y simplicidad, el factor de R se tomó como 1 y su apariencia se ignoró de manera efectiva.
Al multiplicar los diversos factores derivados de toda la serie P, Q, R, ... ahora se obtuvo un factor compuesto que cuantifica la evidencia de toda la columna a favor o en contra de la verdad de A. Con estos factores, se podrían hacer comparaciones objetivas: si un aditivo especulativo que produjo un grupo bueno muy fuerte, pero poco más fue más o menos plausible que otro que produjo una serie de medianos. Los umbrales se establecieron, empíricamente, y variaron a la luz de la experiencia, para el tamaño del factor compuesto que justificaría confirmar un aditivo especulativo como verdadero o enviarlo para un estudio más detallado. Se logró un equilibrio entre la confirmación de suficientes aditivos para avanzar rápidamente y la confirmación de tantos que se produjeron demasiados errores.
La siguiente etapa fue reemplazar el factor de cada buen grupo por el logaritmo de ese factor; y, nuevamente, el comercio de un grado de precisión por velocidad y simplicidad, para escalar y redondear los logaritmos a un conjunto de "puntajes" de números enteros de dos dígitos. Se tabuló un "libro de puntuación", que da la puntuación de cada grupo bueno conocido. De este modo, la multiplicación que consumía tiempo fue reemplazada por una adición lo suficientemente simple como para hacerla mentalmente o con un lápiz. Y los umbrales se transformaron de manera similar en sus equivalentes logarítmicos escalados.
De este trabajo preparatorio surgió un procedimiento simple. El trabajo simplificado, realizado por los civiles y Wrens, fue:
- elimine una columna restando el aditivo especulativo de cada grupo cifrado a su vez;
- comprobar si los grupos descifrados resultantes escaneados; si todos lo hicieron, mire cada uno en el libro de puntuaciones y anote su puntuación si estaba allí;
- agregue los puntajes y, si el total alcanzó el umbral, regocíjese, escriba ese aditivo como se confirmó y pase al siguiente.
El sistema cumplió de manera muy satisfactoria su propósito previsto de probar de forma rápida y sistemática las masas de aditivos especulativos y seleccionar aquellos que probablemente eran ciertos. Nunca se vio como haciendo todo el trabajo. Los casos limítrofes, o los mensajes de preocupación particular, podrían entregarse para un estudio más intensivo en otras partes del equipo. Un ojo observador y una memoria aguda a menudo pueden encontrar un significado donde la aritmética sola no pudo. Y, como siempre en el criptoanálisis, el presentimiento imaginativo basado en la experiencia a veces puede hacer la contribución más importante de todas.
Diversidad en Bletchley Park
Una gran diversidad de mentes se comprometió en Bletchley Park. Sería un error suponer que los criptoanalistas eran todos matemáticos.
Los clasicistas también abundaron. Dilly Knox, la criptoanalista estrella de la Sala 40 en la Primera Guerra Mundial y de Bletchley Park en la Segunda, fue la primera (y última) paleógrafa especializada en escritura antigua. Todo el personal (más de 7000 en el pico) abarcaba desde miles de teleprinters que operaban, la instalación de Hollerith, las bombas Enigma que rompían las teclas y las varias computadoras Colossus durante todo el día hasta un Dilly que trabajaba solo con lápiz y papel. Los civiles en la nómina del Ministerio de Relaciones Exteriores se mezclaron en equipos con hombres y mujeres de los tres servicios. La edad y el rango ocuparon el segundo lugar a los que tenían el don. Y el regalo vino de diversas fuentes. El jefe conjunto del equipo JN 11 de al lado, el capitán de inteligencia del ejército Brian Augarde, era un clarinetista profesional de jazz.
En el trabajo fuimos compartimentados por razones de seguridad y nunca comparamos las notas con otros equipos. Fuera de servicio nos mezclamos libremente. Casi sin contacto con la gente de Bletchley y las aldeas circundantes, y la mayoría de nosotros lejos de nuestras familias, éramos una sociedad muy introspectiva. Todos los hombres civiles (excepto algunos de los más veteranos) tenían que servir en la Compañía de la Guardia Nacional de Bletchley Park: esto era un gran mezclador y nivelador. En el lado intelectual, el ajedrez fue probablemente el círculo más brillante, con Hugh Alexander, Harry Golombek y Stuart Milner-Barry en su centro. Estos tres habían estado juntos en el equipo británico en la Olimpiada de Ajedrez en Argentina cuando comenzó la guerra en septiembre de 1939. Había música de alta calidad. Myra Hess visitó para dar un recital. Actuaciones montadas dentro del personal incluyeron "Dido y Eneas", El quinteto de jazz de Brian Augarde y varias revistas satíricas. Un grupo de nosotros fuimos a menudo en tren y en bicicleta al Shakespeare Memorial Theatre en Stratford-upon-Avon. El baile escocés del país floreció El Salón, que se construyó fuera de la valla de seguridad del perímetro para que la gente de Bletchley también pudiera usarlo, ofrecía bailes, espectáculos y un cine. Una ocasión memorable fue la exhibición deMunchhausen , en color (probablemente la primera película en color que la mayoría de nosotros habíamos visto) y en alemán sin subtítulos. No escuché ninguna explicación de cómo llegó a ser en Bletchley Park. Dudo que fuera a través de los canales de distribución normales.
Bayes y enigma naval alemán.
El criptoanálisis del enigma naval alemán fue significativamente más complejo que el de la JN 25. Muy simplificadora, la máquina Enigma contenía tres (luego cuatro) ruedas de 26 letras en un solo eje, y un tablero de 26 letras; cada rueda podría estar en cualquiera de las 26 posiciones diferentes en relación con sus vecinos, lo que resulta en un número astronómico de posibles combinaciones, y cada combinación se usó para codificar una sola letra del mensaje. La recuperación de estos ajustes de la rueda, que cambiaban diariamente, fue el corazón del proceso de descifrado. Nuevamente menciono solo a tres de las muchas personas involucradas: Alan Turing, quien no necesita presentación; Hugh Alexander, quien además de ser campeón de ajedrez británico era a la vez un maestro de criptoanalistas y un maestro de criptoanalistas; y Jack Good, matemático y más tarde profesor de estadística en Virginia Tech.
Una máquina de codificación alemana Enigma. Cortesía de Bletchley Park Museum
Una máquina de codificación alemana Enigma. Cortesía de Bletchley Park Museum
A diferencia de JN 25, el cifrado Enigma no comenzó transformando los textos de los mensajes en grupos de códigos. Los mensajes fueron cifrados por la máquina, letra por letra, y con el cifrado de cada letra, la configuración de la rueda de la máquina cambió automáticamente antes de cifrar la siguiente. Al igual que con JN 25, una etapa temprana importante del criptoanálisis fue establecer una profundidad.
El análisis comienza con dos mensajes conocidos de sus indicadores que tienen dos de las tres configuraciones de ruedas en común. El objetivo inmediato es identificar el tercero. Los mensajes pueden deslizarse uno contra otro, hasta 25 lugares a la izquierda o a la derecha; y en cada una de estas 50 alineaciones habrá un tramo de letras una sobre la otra. Esta es la "superposición". Los mensajes ya tienen dos configuraciones de rueda en común: una de las 50 alineaciones debe corresponder a tener la tercera en común también. En esa posición, todos los pares de letras en la superposición se habrán cifrado exactamente igual. Los mensajes están entonces en "verdadera profundidad". Turing notó, posiblemente a principios de 1939, que podía establecer cuál de las 50 alineaciones probablemente daría la verdadera profundidad mediante la explotación estadística de dos observaciones simples:
Si las frecuencias de las 26 letras del alfabeto en lenguaje sencillo son f 1 , ..., f 26 , la probabilidad de que dos letras seleccionadas independientemente sean las mismas, es decir, coincidirá, es
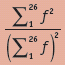
Esta es la relación de repetición o tasa de repetición: el anverso de la diversidad. Tiene mucho en común con la 'característica' de Udny Yule basada en las frecuencias de palabras que ideó al abordar la cuestión de la autoría de Thomas à Kempis de De Imitatio Christi 7 . Llamé a Udny Yule en St John's College, Cambridge, en 1946: una pequeña figura con una gorra en la enorme y alta habitación de Fellow's Room. Hablamos de su característica como medio de análisis del lenguaje. Por supuesto Bletchley Park no fue mencionado. Pero, teniendo en cuenta cuántos matemáticos de Cambridge habían estado trabajando allí, me preguntaba si sabía más de lo que se suponía.
Usando las frecuencias de letras citadas en Wikipedia, obtenemos tasas de repetición de 1 en 15.3 para el inglés y 1 en 13.1 para el alemán. El equipo de Hut 8 utilizó 1 de 17, probablemente derivado de una gran muestra de mensajes navales alemanes. (El lenguaje naval será diferente del lenguaje normal). Dos letras elegidas independientemente al azar tienen una tasa de repetición de 1 en 26. Por lo tanto, el evento de una sola letra que coincida entre los dos mensajes tendrá una probabilidad de 1/17 si la hipótesis de un la alineación correcta es verdadera, y una probabilidad de 1/26 si es falsa. El teorema de Bayes luego nos dice que las probabilidades previas en la hipótesis se multiplicarán por un factor de 26/17 o 1.53 para dar las probabilidades posteriores después de ese evento. El evento alternativo de letras que no coincidan entre los dos mensajes tendrá una probabilidad 16/17 si la hipótesis es verdadera y una probabilidad 25/26 si no lo es; dando un factor de (16 × 26) / (17 × 25) = 0.979, reduciendo ligeramente las probabilidades previas en la hipótesis. Además, como los sucesivos sucesos a lo largo de la superposición de los dos mensajes son independientes para fines prácticos, sus factores se pueden multiplicar para obtener un factor compuesto para la alineación como un todo.
Tomemos como ejemplo la prueba de una alineación de dos mensajes con una superposición de 32 letras, que arrojaron 7 pares que coincidieron y 25 que no. El factor Bayes compuesto para esto es 1.53 7 × 0.979 25 = 11.5 a favor de que esta alineación sea correcta. Las probabilidades anteriores de 1 a 49 (porque había 50 alineaciones igualmente probables antes del evento) se convierten en probabilidades posteriores de 1 a 4.3.
Para simplificar el manejo de los muchos factores de Bayes producidos, a la velocidad requerida, Turing trajo la unidad de decibeles 6 . Esto se usa familiarmente para medir la sonoridad, pero no se limita a eso. Su definición generalizada es una décima parte del logaritmo en base 10 de la relación de dos medidas de cualquier cantidad que se pueda medir. El uso de la unidad de decibeles trae la simplificación de que multiplicar las proporciones da lugar a la simple adición de sus decibeles. Así que era precisamente apto para manejar el factor de Bayes, la proporción de dos probabilidades. Extendiendo el lenguaje adoptado de Banbury (ver texto principal), Turing cambió el nombre de la unidad de decibel a deci Ban. Más tarde, cambiando un grado de precisión por facilidad y velocidad, la unidad utilizada se cambió a medio deciBan o hdB y las medidas se redondearon a números enteros.
Continuando con el ejemplo anterior de 7 coincidencias en una superposición de 32 letras, el logaritmo de base 10 del factor 11.5 fue 1.061, por lo que se midió como 21.2 hdB, que se redondea a 21. Esto se conoce como el "puntaje" de la alineación.
- si dos letras, una encima de la otra en los mensajes cifrados, fueran iguales, es decir, si "coincidían", y la alineación era correcta, entonces (porque la misma configuración de la máquina las había cifrado) las letras correspondientes en el plano original los textos también deben coincidir;
- Debido a que las frecuencias de las letras en el lenguaje se distribuyen de manera desigual, la coincidencia se producirá con más frecuencia en profundidad verdadera que en falsa.
En otras palabras, un mensaje puede distinguirse de un revoltijo aleatorio porque las frecuencias de letras son diferentes. Esta diferencia se ocultará en los mensajes codificados, pero volverá a aparecer, cuando los mensajes codificados estén correctamente alineados, en las frecuencias de los pares correspondientes (ver recuadro).
Se tomaron medidas prácticas para convertir esta declaración estadística en un procedimiento que podría ser seguido por personal no matemático en la escala ya la velocidad requerida. Contar el número de pares coincidentes involucrados en la grabación de los mensajes en hojas de papel pesadas impresas con hasta 250 alfabetos A – Z verticales: esto se hizo perforando un agujero en la posición de cada letra en columnas sucesivas. Las dos hojas se deslizaron una contra la otra sobre un fondo iluminado para reproducir sucesivamente las 50 alineaciones. En cada posición, las letras coincidentes aparecían como agujeros visiblemente coincidentes, para ser contados y registrados para esa alineación. Como las hojas se imprimieron en Banbury, se llamaron Banburies, y todo el proceso comenzó así como Banburismus. Más detalles sobre la ruptura de los cifrados Enigma se dan en la versión del sitio web de este artículo,www.interscience.wiley.com/journal/significance .
Es interesante observar que tanto el simple procedimiento visual como el diestro con Banburies y el mecanizado a alta velocidad de la máquina de Hollerith explotaron los orificios perforados en las tarjetas. Ambos se derivaron del dispositivo de tarjeta perforada del telar Jacquard 1801, que atrajo a Ada Lovelace cuando visualizó la computadora moderna en 1843. Su visión se realizó en Colossus. Bletchley Park usó tanto la primera computadora como el dispositivo que la había inspirado 100 años antes.
Todo lo anterior es una descripción simple y simplificada del procedimiento, pero es suficiente para demostrar el papel jugado por el teorema de Bayes. Para ponerlo en perspectiva, solo fue el comienzo de la ruptura diaria de la configuración de la rueda Naval Enigma. Con las posibles alineaciones para un par de mensajes calificados, todavía era a menudo una cuestión de juicio elegir la correcta: otras técnicas, criptoanalíticas más que estadísticas, aportaban experiencia. Bayes proporcionó solo la plataforma desde la cual se inició la recuperación de la configuración diaria de la rueda.
Cuando terminó la guerra, Hugh Alexander y muchos otros se quedaron con la organización cuando se mudó a Cheltenham como la Sede de Comunicaciones del Gobierno. Los dons volvieron a Cambridge y Oxford. Stuart Milner ‐ Barry regresó al Tesoro y más tarde fue el oficial de ceremonias del gobierno. Max Newman y Alan Turing continuaron desarrollando computadoras en la Universidad de Manchester, pero Tommy Flowers regresó a Dollis Hill sin reconocer que había hecho algo fuera de lo común.
Otros iban en direcciones menos previsibles. Edward Boyle y Roy Jenkins entraron en la política y el gobierno. Henry Reed, un lingüista japonés mientras estaba en nuestro equipo de JN 25, volvió a la poesía, los juegos de radio y la BBC. Su "El nombramiento de partes", que ha sido llamado "el poema más amado y más antologizado de la Segunda Guerra Mundial", expresa sus reflexiones mientras servía en la Guardia Nacional de Bletchley Park. Angus Wilson se convirtió en un novelista aclamado. Colin Thompson se convirtió en Director de las Galerías Nacionales de Escocia, y Peter Benenson fundó Amnistía Internacional. Peter Laslett se convirtió en un historiador social de Cambridge e inició la Universidad Dawn, de la cual surgieron la Universidad Abierta y la Universidad de la Tercera Edad.
En el obituario de Jack Good, The Times escribió: “Para los estadísticos, Good es uno de los padres fundadores de las estadísticas bayesianas. Este enfoque fue poco utilizado antes del trabajo de Good, pero recibió un impulso importante gracias a su libro de 1950, Probability and the Weighing of Evidence 6 . La importancia de Good fuera del mundo académico radica en que ha sido una figura clave en el equipo matemático de Bletchley Park ” 8. Así, en relación con Bayes, como en el desarrollo de las computadoras, la contribución de Bletchley Park continuó desde la guerra hasta la paz.
Hut 1 en Bletchley Park. Fue desde edificios como estos en los terrenos de la mansión que se realizó el descifrado de códigos. Bletchley Park es ahora un museo y sitio de patrimonio abierto todos los días para los visitantes. Los detalles se pueden encontrar en www.bletchleypark.org.uk . (Fotografía de Toby Oxborrow.)
Hut 1 en Bletchley Park. Fue desde edificios como estos en los terrenos de la mansión que se realizó el descifrado de códigos. Bletchley Park es ahora un museo y sitio de patrimonio abierto todos los días para los visitantes. Los detalles se pueden encontrar en www.bletchleypark.org.uk . (Fotografía de Toby Oxborrow.)
Referencias
- 1 Simpson, EH ( 1949 ) Medición de la diversidad . Naturaleza , 163 , 688.
- 2 Simpson, EH ( 1951 ) La interpretación de la interacción en la tabla de contingencia . Diario de la Royal Statistical Society (Serie B) , 13 , 238–241.
- 3 Copeland, BJ ( 2006 ) Colossus: The Secrets of Bletchley Park's Codebreaking Computers . Oxford: Oxford University Press.
- 4 Smith, M. y Erskine, R. ( 2001 ) Action This Day , pág. 185. Londres: Bantam Press.
- 5 Alexander, CH O'D. ( c . 1945 ) Historia criptográfica del trabajo sobre el Enigma naval alemán, PRO HW 25/1 y http://www.alanturing.net/turning-archive
- 6 Bien, IJ ( 1950 ) Probabilidad y el peso de la evidencia . Londres: Charles Griffin.
- 7 Yule, GU ( 1944 ) El estudio estadístico del vocabulario literario . Cambridge: Cambridge University Press.
- 8 The Times , 16 de abril de 2009 .





